Timer LLC

The inverse problem and its solution for GROT type ground penetrating radars

The physical work principles of all georadars are the same. To get the information about the medium it is necessary to solve the inverse problem. The solution of the three-dimensional inverse problem of creating the image of the subsurface soil structure is extremely difficult because of great computing resources being needed. At the same time, it is the solution of the inverse problem in the complete formulation, which means that it is based on the Maxwell's equations sampling and sustainable solutions finding, that allows automating the process of data interpretation of GPR scanning.

The inverse problem in georadiolocation is the task of recovering the values of the medium parameters from the GPR scanning data.

All inverse problems are improperly posed, which means they don't meet at least one of the following conditions:

• the existence of the solution
• the uniqueness of the solution and
• its stability regardless relatively small perturbations of the scanning data (that is being sustained to the input data disturbances)

The solution of the direct problem is finding the consequence of a certain process using the information about its well-known reason. For example, it is possible to calculate the parameters of a medium (with or without inhomogeneities) with a certain electromagnetic pulse propagating in it, if the parameters of the pulse and the environment are known. In addition, the solution of the direct problem allows calculating the dynamic range of the georadar pulse needed to detect specific inhomogeneities.

Unlike the direct problem solution, the solution of the inverse problem is difficult because different causes or combinations of them can lead to the same effect. Sometimes a set of factors may even disguise the searched effect. For example, in many cases, when in winter pounds and reservoirs are scanned with georadars with low resolution, instead of two boundaries (between ice and water, water and the bottom) only one is shown (between water and the bottom), and the distance to it is distorted. Also, when locating inhomogeneities (for example, to find pipes), errors, related to the overlay of the effects, which can be caused by the presence of the trenches, can occur. In addition, the degree of noise coherence in the radar should be taken into account too, as it often leads to the appearance of false objects during the GPR scanning data interpretation.

So far the basis for the georadiolocation data interpretation is the principle, according to which the distance to the reflecting object is determined by the delay times of the reflected scanning pulse with respect to the moment of its emission. The amplitude of the reflected pulse depends on the radio waves absorption of in the medium and the reflection coefficient at the boarders between the media. To interpret the georadiolocation data, the laws of geometrical optics are used. 1

This kinematic model, which is based on the ray theory of wave propagation and used in GPR data interpretation, can be used to solve the inverse problem, when the scanning pulses have relatively short wavelengths and the media conductivity is low. If wavelengths of the pulses are long and the medium conductivity is high, the ray theory should be used with caution and the parameters of the ground penetrating radars should match the peculiarities of the signals propagation in the real medium.

The GPR scanning pulses in real media can have the characteristic times, which are comparable to the times of the medium polarization mechanisms appearance with respect to the moment of the scanning pulse emission. Changes not only in the amplitude but also in the pulse waveforms during its propagation in the real media lead to the necessity of forming the receiver units linear characteristic, used to digitize the reflected pulse, during the construction of the georadar. For example, the frequency and temporal gating procedures lead to additional signal distortions and therefore to errors during the data interpretation. The pulse characteristics during its propagation in different media depend on the method of their estimation. [2,3] For example, the empirical data, which is often used to estimate the scanning and irregularities depths, on the attenuation of the pulse with a particular frequency cannot be considered a reliable basis for the analysis of the maximum possible research depth, if the exact ground penetrating radar parameters are unknown. To correctly estimate the values of the parameters of the medium during the qualitative and quantitative GPR scanning data interpretation be taken into account the impact of the georadar parameters, such as its power, length and leading edge steepness of the transmitted pulse, the analogue-to-digital converter digit capacity and frequency, linearity of the receiver characteristics as well as parameters of the antennas that influence the frequency range and the dispersion dependence of the broadband pulse.

The solution to the problem of the subsurface soil structure modelling with the usage of the ground penetrating radar data requires taking into account a large set of the parameters and a high level of interpreter professionalism. The solution of the ill-posed problem deals with its complete specification and determination. These procedures require additional priori information based on the research experience and experimental data. Using GPR scanning experience, the researcher selects the optimal simplifying model to interpret the new data.

Simplifying models in georadiolocation

Different simplifying models are used in georadiolocation, such as the following:

• The model that describes the electro-magnetic field in the framework of the wave approximation and uses the delay times of the reflected signal to determine the structure of the medium. In this model, we can use the deconvolution methods, the Hilbert transform, accumulated through research algorithms, which are used in seismic exploration, etc. 1If the data can be interpreted in the framework of this model, the interpretation provides monosemantic results, when the scanning pulse has a triangular shape on radargrams. This model of a high-frequency approximation is not very effective in media with high conductivity, and that is why the use of certain ground penetrating radars is inefficient for low-resistant media studies even today.

• Depending on the operating frequencies range of the probe pulse, a high-frequency and low-frequency approximations in the solution of Maxwell's equations are used, in which the dielectric permittivity models can be used to simplify the equations by neglecting some of the parameters. This approach is a good regularizing algorithm to produce the quality results. This approach simplifies the solution greatly. [2,3]

• One-dimensional and two-dimensional approximations, which in some cases can be used to get the analytical solutions and thus to find characteristic qualitative and sometimes quantitative features of the solution.

The use this or that model requires a high professionalism of the interpreter, because each of the studied through the GPR data interpretation media is diverse. The wrong choice of the simplifying model leads to the incorrect solution.

The need to improve the quality of diagnostic and identification of sub-surface areas and objects processes, based on the results of georadar scanning, and the intention to ease the job of the GPR data interpreter and, ideally, to obtain the solutions of the problems automatically lead to the necessity of solving the inverse scattering problems in its most complete three-dimensional formulation.

As it is known, the inverse problem georadiolocation can be set on the basis of the complete formulation of Maxwell's equations. Until now, the universal solution to this problem is not obtained, although approaches to exist quite a few. 4

It is well known that the solution of the problem in its general formulation requires significant computing power and a lot of time to perform the necessary calculations, while for georadiolocation the real-time data processing, directly during the GPR scanning process, is rather essential. We have concentrated a part of our efforts on these important aspects of geoscanning.

Our approach to solving the three-dimensional inverse problem in georadiolocation

Solution of this problem and Maxwell's equations is based on adaptive grids. The main difficulty, when solving such problems, is to sample Maxwell's equations on the given uneven grids correctly, when solving ill-posed rarefied systems of equations with many unknown parameters and values.

To solve this problem on the basis of numerical modelling of Maxwell's equations, we offer two types of grids:

Tensor grids

This type of grids allows presenting the matrixes in the problem of least squares in the form of multilevel-block-Toeplitz. This reduces arithmetic needs and memory requirements. At the same time, for a more accurate presentation of the required object, you need to grind grid greatly and introduce special regularizers that may worsen the solution quality.

Voronoi-Delaunay adaptive polyhedrons

Using such grids, we get a more stable presentation of the object under study. At the same time, unstructured grids require special multilevel and hierarchical matrix methods, which are different from the method of the fast Fourier transformation.

Developed for solving the systems of equations and successfully applied by our partners from "Elegant Mathematics" LTD for more than 15 years iterative methods allowed us to find the most suitable and sustainable method of solving linear systems of equations and, if necessary, to regularize invertible matrixes.

These algorithms are were used by the Maui High Performance Computing Center (MHPCC) DSRC (USA, Hawaii) on behalf of the Mobile company to solve the ill-posed equations systems of similar type with rarefied regularization using the massively parallel computers.

The amounts of used computer memory and time are proportional to the amount of calculations required to model the object and to the spatial resolution of the grid. Application of the advanced computing algorithms, developed in recent years, has made it possible to solve such problems for large amounts of unknown parameters that describe the object spatial structure with the desired grids resolution.

We have made the solution algorithm flexible enough to be able to take into account the priori information, so that any priori information could be used as a regularizer.

For example, the program, which uses our algorithm, can interrupt the solution iteration after analysing preliminary solutions using the visualization software. Schematically, the solution deals with the comparison of the measured field on the surface with the calculated set of fields, which are the result of the solving of the direct problem of pulse propagation in the medium process with the given distribution of the electromagnetic parameters.

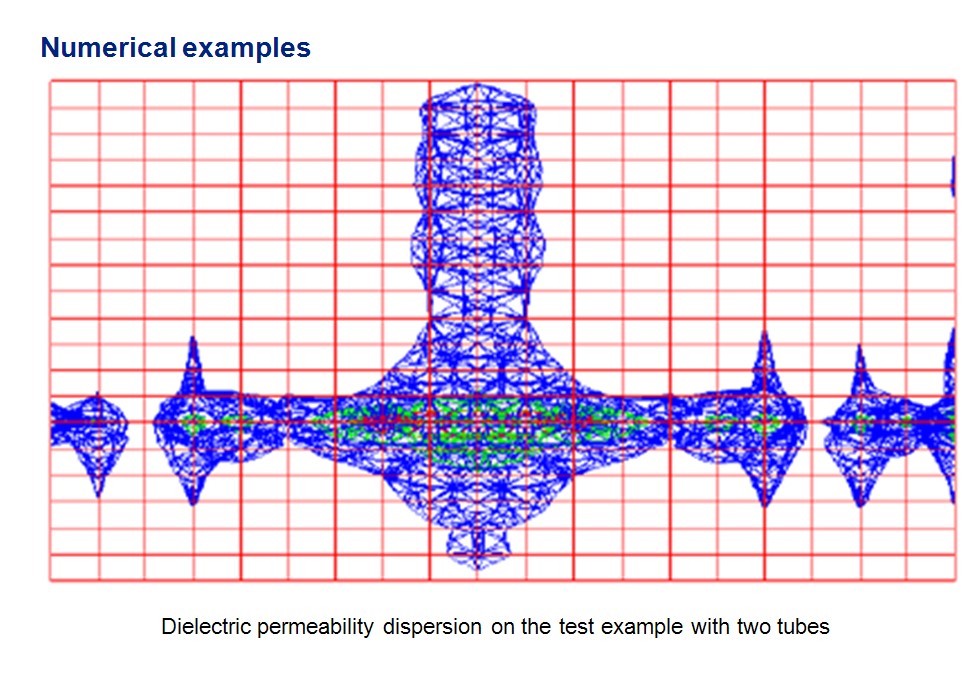
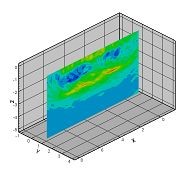
The measurement error estimation can be carried out through the solution of the direct problem with the given value of grid resolution. For example, two metal objects (pipes) can be placed perpendicular to each other in a homogeneous medium. For the selected pipe diameter, which is to be twice as big as the value of grid resolution, the solution can be presented on two-dimensional and three-dimensional diagrams and gives the measurement error value for the given set of parameters.

The result of the solution in a three-dimensional form In particular, the images demonstrate the dependence of the solution accuracy on the antenna polarization. So, when the experiment is being planned, the right scanning technology can always be selected to get the required accuracy of the results. The solution has been successfully tested in archaeology.

Figure 3 illustrates an example of solving a three-dimensional inverse problem of the inhomogeneous inclusion locating in archaeology. It is important to point out that the solution of the equations system with 10000 unknowns was obtained within a few seconds of machine time with an ordinary personal computer, directly at the place of the GPR scanning. This example was chosen for the presentation, because after the GPR scanning and data interpretation there were excavations in that area, and it was confirmed that the inverse problem solution results had the accuracy of 10 cm. The increased complication of the problem, caused by the increased size of the object being studied and, therefore, by the increase in the number of unknowns in the inverse problem equations system, for example, of up to 1000000, increases the computation time to 1 hour. So, modelling a three-dimensional structure of the scanned media directly in the field is possible.

Figure 5 illustrates a three-dimensional model of the studied media in the GROT12 program.

In conclusion, we would like to mention that our approach to solving the three-dimensional inverse problem in georadiolocation allows us to successfully use GROT type ground penetrating radars to solve the most complex problems, which has been confirmed by numerous experiments, in real time.

REFERENCES

1. Starovoytov A. V., Vladov M. L., GROUND PENETRATION RADAR SOUNDINGS OF SHALLOW SUBSURFACE, M.V. Lomonosov Moscow State University, Moscow, Russia, 1999, 92 p.
2. Rudenchik E. A., Volkomirskaya L. B. and Reznikov A. E., Investigation of the Propagation of Signals in One-Dimensional Electrodynamics for interpretation Electromagnetic Sounding Data. Consideration of the Analytic Properties of Permittivity, Physics of Wave Phenomena, 2008, Vol. 16, No. 1, pp. 1-18. © Allerton Press Inc., 2008.
3. Rudenchik E. A., Volkomirskaya L. B. and Reznikov A. E., Investigation of the Propagation of Signals in One-Dimensional Electrodynamics for interpretation Electromagnetic Sounding Data Consideration of Conductivity in the Function of Permittivity, Physics of Wave Phenomena, 2008, Vol. 16, No. 2, pp. 1-14. © Allerton Press Inc., 2008.
4. The subsurface radiolocation questions, ed. Dr. Sc. Grinyov A. Yu., Moscow, Russia, 416 p., Radiotekhnika, 2005
5. Volkomirskaja L. B. , Reznikov A. E., Ibragimow I. V. and Ibragimowa E. I., The International Conference on Mathematical Methods in Geophysics «MMG-2008», Novosibirsk, Russia, October 13-15, 2008, MMG 2008
6. Volkomirskaja L. B. , Reznikov A. E., Ibragimow I. V. and Ibragimowa E. I., Investigation with GROT 12 3D Radars and Real Time Solution of 3D Ground-Penetrating Inverse Problem. GPR2008, Birminghem, July 15-19, 2008
7. Volkomirskaya L. B., Ibragimow I. V., Ibragimowa E. I., Varenkov V.V., Reznikov A.E., Rudenchik E.A., Sahterov V. I., Solving the three-dimensional inverse problem in georadiolocation using GROT 12 type GPR data, Abstracts of the 4th International Conference «Engineering and Mining Geophysics - 2008», Gelendzhik, Russia, "InjGeo-2008", April 25-30, 2008